Math Fluency - both Facts and Procedures

Pentucket has demonstrated some impressive growth with math performance of our students since adopting a coherent and consistent math program in 2017. While not everything is perfect and addressed with a program, the district has worked to address areas that needed additional attention, and with the transition to Eureka Squared in 2023 from the first version of Eureka, most areas of concerns were addressed. Regardless of the program used though, improving student fluency with math, both fact fluency and procedural fluency, has been a key focus point in all math classrooms, from Kindergarten through grade 8.

In the May 1, 2023 Ed Week article - misconceptions around fact fluency were addressed, including the simple aspect around their importance. 

“Those skills help kids advance when multi-digit arithmetic, fractions, and long division enter the picture—allowing them to focus on more complex problem-solving instead of simple computation.”

While memorizing math facts is a long taught strategy, not every aspect of fluency relies purely on memorization. For example some people may be able to memorize most of the multiplication facts and can quickly get to an answer for the few they don’t have memorized. That strategy is effective for them so long as it does not prevent them from tackling more complex math. 

There is always debate over timed activities. Some people have written and conducted studies concluding that timed math activities are the cause of “math anxiety” in students. However the research does not really indicate that. The What Works Clearinghouse, which develops guides for schools and teachers based volumes of research rather than a single study, identifies regular use of timed activities as 1 of 6 key practices in their 2021 publication Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades.

In addition to basic facts, timed activities may address other mathematical subtasks important for solving complex problems. This could include, for example, recalling equivalencies for fraction benchmarks of 1/2 and 1, which helps students compare the magnitude of fractions or solve rate problems more efficiently. It can also help to quickly evaluate and estimate place value, which helps students identify whether regrouping is needed.

Recommendation # 6 specifically addresses the topic of timed activities. The research associated with this document clearly identifies that timed activities are necessary when solving double-digit addition and subtraction problems. “The goal of these activities is to move students toward accurate and efficient performance of these smaller mathematical tasks so that this knowledge can be easily accessed when necessary for solving problems.” 

The panel that conducted the research and developed the guiding document does not recommend merely giving students timed worksheets or putting students on a computer-based program without supporting their learning. Timed activity can engage students by providing feedback in real time, including goals for improvement, and steadily increasing item difficulty. Timed activities can be structured similarly during intervention, regardless of whether the focus is on automaticity with basic arithmetic facts or problem solving.

The recommendation is for teachers to think about how they could set your students up for success. Our staff considers these questions when preparing for math fluency building activities as activities that support fluency need to address these elements to be effective: 

• Does the timed activity make sense for the intervention focus? 

• Do your students have a way to find the answer if they don’t know it automatically? 

• Are you giving students feedback in an immediate and meaningful way? 

• Are students observing their own progress and setting goals? 

For many years, schools have avoided timed activities because they had come to believe that it causes anxiety and a “fear”  of math. In fact, the research that has indicated some anxiety may be caused by math timed fluency activities, is based on students using worksheets with a large number of problems on them. This is a practice we have sight to avoid when teaching fluency. 

Recent PD on Math Fluency

For the past two years the K-5 teachers and 6-8 math teachers have been engaged in a variety of professional learning activities mostly centered on the book Figuring Out Fluency in Mathematics by John SanGiovanni and Jennifer Bay-Williams. SanGiovanni also spent a full day in the District in November of 2024 providing professional development around the concepts in the book with procedural fluency but also for all staff around productive struggle. After multiple rounds of book studies, the concepts and activities have become commonplace in classrooms and have paired well with the implementation of Eureka Squared.

A great deal of the fluency work the students are engaged in involves games. So naturally, many students don’t mind participating and likely don’t find it to be much of a chore.

Donaghue School 4th Grader, Matthew Scarsella described how he enjoys the games. 

“We use dice at various times during the week in stations or with a partner to practice our multiplication and division skills. I can be really competitive so I enjoy the games because I know it challenges me to get better and more fluent.” - Matthew Scarsella - 4th Gr.

Fluency building - more than timed worksheets

Some of the games the students play require them to think about the most efficient way to complete basic math facts. While some are games that involve timing, most of the learning and practice is not timed. This gives the students an opportunity to think and become more automatic with math facts or solving basic math problems. 

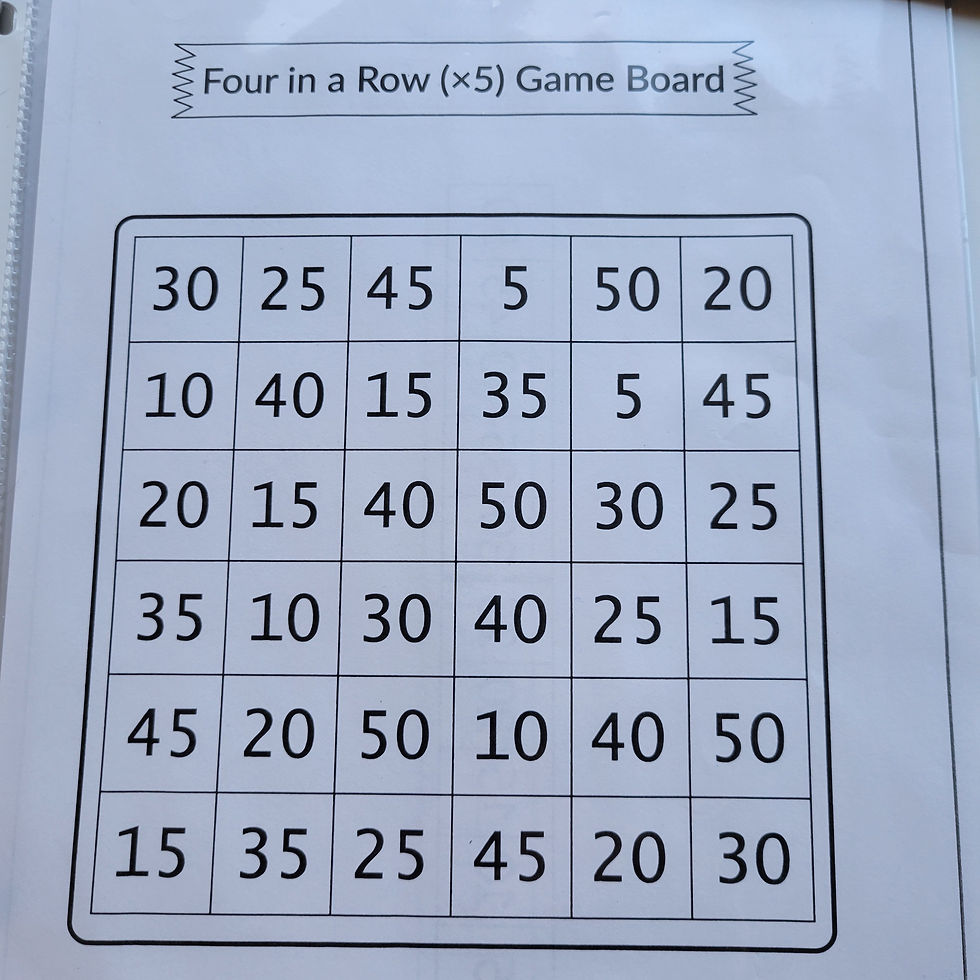
The two images above show 4th grade math fluency building games that have students building multiplication fact fluency. This differs from the flashcard method and centers the work around a particular number concept, such as multiples of 5. Playing cooperatively with another student has them focusing on their own math, but also seeing and hearing other students with math as well. 

The use of decks of playing cards are great as we can work with numbers through 10 for multiples and factors. There are so many games that kids can play where the directions are essentially the same but the focus multiples or factors will change so the targeted practice is on what particular skill students may need or on what was just taught for the entire class. The multi-sided dice - more than just the typical 6 sides - also allows for greater flexibility with the games. In both cases, the students can move rapidly through many opportunities to practice math facts but while holding playing cards and dice, which hardly feel like they are practicing math.

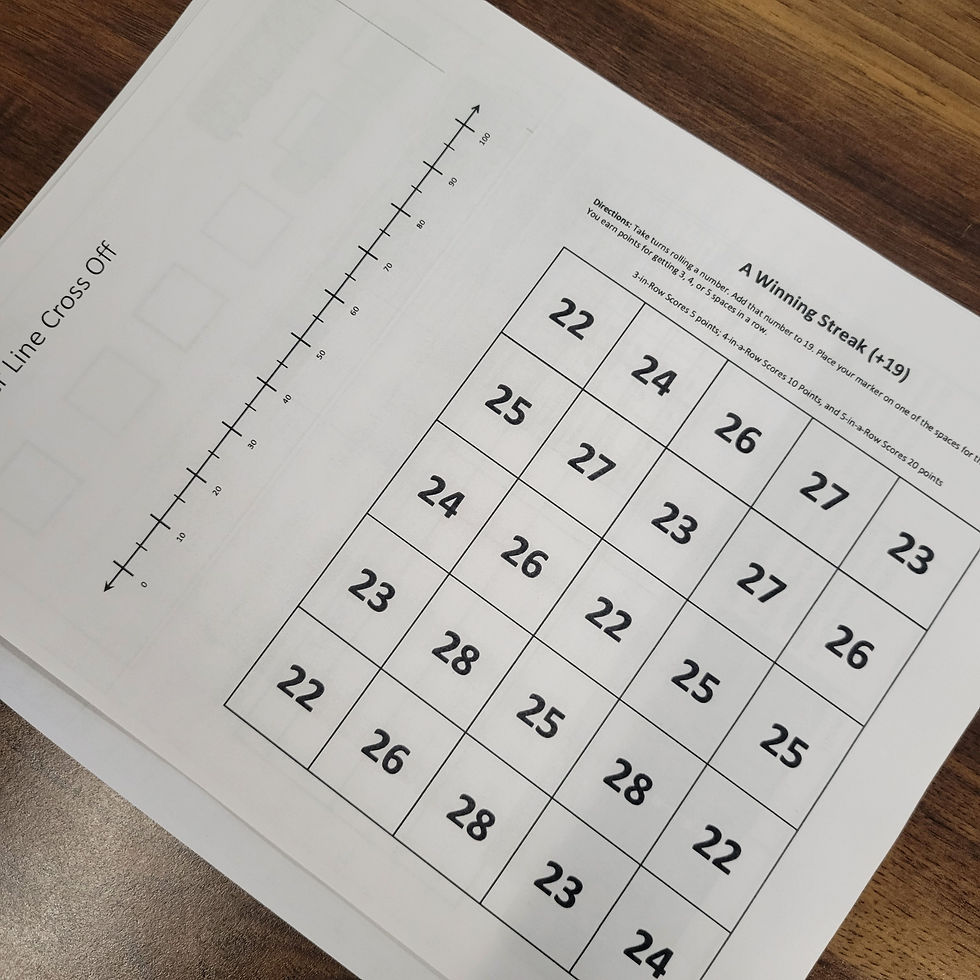
Some other examples of games we have organized for students to play really extends their thinking to become even more fluent with both facts and procedures to solve math problems. The “Winning Streak” game, which was presented to the staff in November at the PD session with SanGiovanni, can be altered multiple ways and flexibly applied for students who need to be pushed at higher levels, but it can also be used with students who are working on more simple facts. The example in the photo below might be used with students in 1st or 2nd grade to build up their additional skills. Rolling a number then adding on to 19, has students starting at a number that requires them to recognize a change in the tens column. The frequency of this in a short window, without the need for speed can be very impactful for students with the repeated practice. Playing the game with a peer and for points makes the practice and the thinking feel a lot less like practice. Teachers have been using games similar to this and frequently changing up the concept for practice, having students focusing on what was just taught, or having it be used as mixed review. 

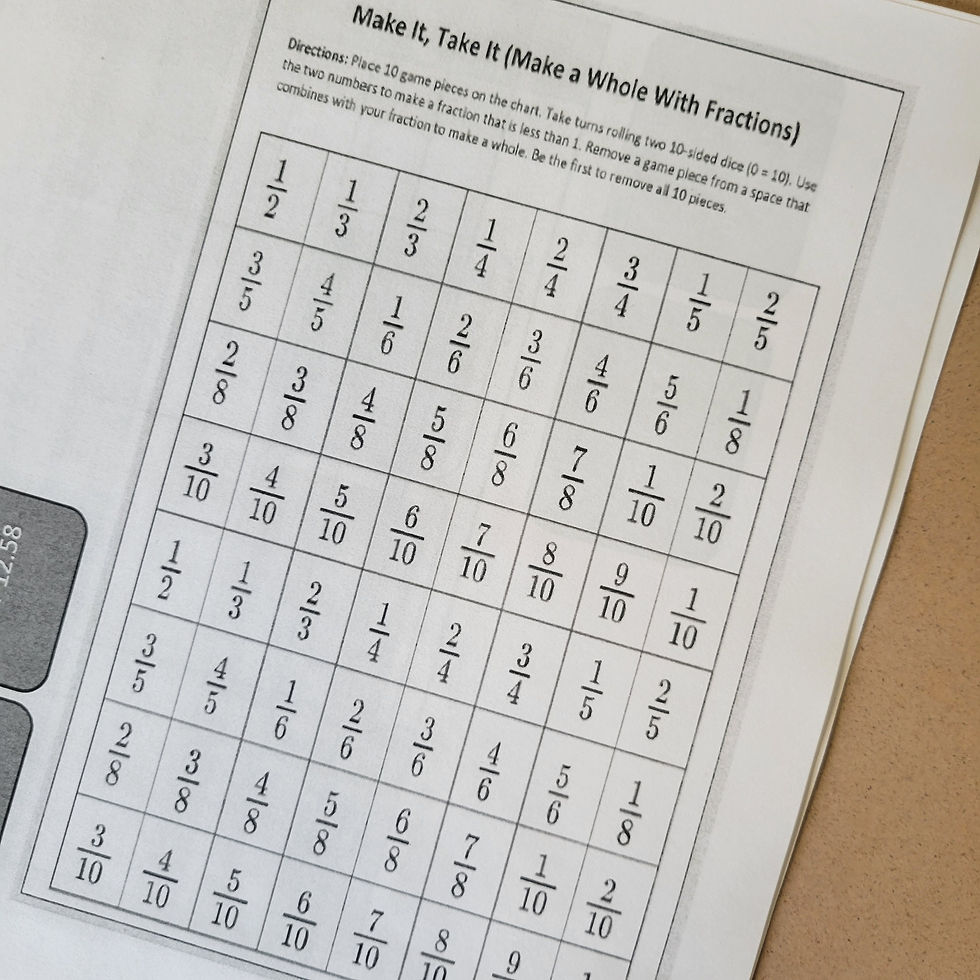
For students in upper elementary grades, we recognize that automaticity extends into understanding factions, decimals and percentages. This is really the gateway into algebra and the more fluid a student is with navigating numbers less than 1, the more easily it opens up doors to apply that knowledge to more complex word problems and real situations. The Make it Take game uses 10 sided dice and has students thinking of ways to make 1 whole. The quickest student to do it 10 times wins. Building fluency with understanding parts of a whole extends a student's thinking of facts into a concept that may seem a bit more abstract. Doing this frequently gives good practice to thinking about how numbers are constructed but also how whole numbers can be deconstructed. 

Using Data 

Beyond the fluency practice and procedural fluency work, our staff have been using data on student performance to help them navigate where more targeted instruction or practice may be needed. Trina Forrest, the 6th grade math teacher at Page Elementary, uses multiple methods to monitor how students are doing with the taught concepts. 

Ms. Forrest outlined how she and her colleagues are using data to drive instruction. Some practical examples include:

• Formative Assessments & Exit Tickets: 

Use daily exit tickets or quick quizzes to assess understanding of key concepts. Analyze student responses to identify common misconceptions and adjust the next lesson accordingly.

• Benchmark Assessments - I-Ready

Use assessment data to create small groups for targeted intervention (e.g., students struggling with fractions get additional practice while others work on enrichment activities. While these groups may be formulated by the benchmark assessment, they are often rotated based on ongoing data collection.

• Error Analysis on Student Work

Collect and categorize student errors from homework or tests to determine patterns. Use this data to reteach specific skills to the whole class or in small groups. Ms. Forrest commented on how this helps tailor lessons to meet the specific needs of students.

“It's easy to mark a problem incorrectly and move on, but the most beneficial instruction takes place when we take the time to understand student thinking. By working directly with students to address misconceptions, we can correct inaccuracies at the source. Identifying patterns in errors through data analysis allows us to make targeted adjustments that lead to meaningful improvements in student learning." - Trina Forrest - 6th gr. Math Teacher at Page Elementary

No matter the math concept, students, like the ones in the photos above, will often complete an exit ticket after a lesson. That exit ticket provides Ms. Forrest or any of the teachers with critical data points on their progress with the concept. When students struggle across the board, the teacher knows to revisit the concept. But when there are only a few students who show difficulty, the teacher has the data point to address it with just those students. For the students in the photo above, they are working with partners to determine areas of polygons on the coordinate grid by decomposing and color-coding shapes.

Specialized instruction 

Somewhere along the way, it started to become commonplace to think that we should limit the number of strategies a student with disabilities is asked to learn for math. The line of thinking was that if we just have them learn one, and do that well, then they will be better off. However, what we know about strategies in general, that having just 1 way to do something or figure something out, is quite limiting and often leads to highly inefficient approaches to doing math.

When we build up student understanding around multiple ways to become fluent, especially those who can begin to memorize some math facts but may struggle with others, we are giving them access to do more complicated math. The point of strategies is to know how and when to use it - strategically - or with purpose. 

In Figuring Out Fluency in Math, SanGiovanni and Williams describe Procedural Fluency as having three core components: Efficiency, Flexibility & Accuracy. Standard algorithms and memorizing facts can certainly lead to efficient work and accurate results. Knowing and understanding math requires additional understanding for flexibility to know how and when to apply strategies to new problems. When all three are connected we build student capacity to work through math fluently. For many students, this seems to come rather effortlessly or with little amounts of practice, yet for others, it requires some very purposeful instruction and targeted practice routines. The more we build those practice routines into the everyday systems in the class, the more engaged our students will be.

Dr. Brent Conway

Assistant Superintendent